도넛 코드

서론

유튜브 알고리즘으로 우연히 “도넛 코드” 라는것을 발견했다.

간단하게 이야기하자면 C언어 기반으로 다양한 수학 함수를 사용하여 일부 특수 문자를 3D 방식으로 회전하는 도넛 형태의 모양으로 명령창에 띄워주는 코드인 것 같다. C언어 뿐만아니라 자바스크립트로도 구현 할 수 있는 것 같아 아래에 한번 구현해보았다.

실행시켜보니 특수한 문자로 구현된 도넛 모양의 3D 모델이 회전하는 것 을 볼 수 있었다. 자세히 보니 코드로 모양을 잡아준것 뿐만 아니라 3D 모델처럼 보이기 위해 명도와 채도까지 신경써서 구현한 것을 파악했다. 비록 문자로 구현되었지만 수학 함수를 사용해서 간단하게 나마 3D 모델이 동작한다는 것이 흥미로웠다.

그럼 어떻게 구현했는지 한번 알아보려고 하며 유튜브 영상과 원문에선 매커니즘을 다음과 같이 설명한다.

이 코드는 프레임버퍼와 Z-버퍼를 기반으로 픽셀을 렌더링하는 방식으로 작동하며 3D 물체를 2D 화면에 투영하기 위해 다음과 같은 과정을 따릅니다.

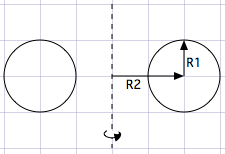
• R2를 중심으로 반지름이 R1인 원을 생성하고
• 그 원을 Y축을 중심으로 회전하여 도넛을 생성하며 그 도넛을 다시 X축과 Z축을 중심으로 도넛을 회전시켜 기본적인 모델을 생성해서 2D 화면으로 도넛을 보여줍니다.

• 도넛 모델에 조명을 부여하기 위해 표면의 법선 벡터를 계산하고 그것을 통해 빛의 방향과 표면 방향 사이의 각도를 계산하여, 이를 기반으로 픽셀의 조명 값을 결정합니다.
• 마지막으로 픽셀의 조명 값을 모델에 부여하여 완성합니다.

이러한 구현 방법을 다음과 같은 실제 코드로 만들어 준다.

• C 코드

                k;double sin()
            ,cos();main(){float A=
          0,B=0,i,j,z[1760];char b[
        1760];printf("\x1b[2J");for(;;
      ){memset(b,32,1760);memset(z,0,7040)
      ;for(j=0;6.28>j;j+=0.07)for(i=0;6.28
    >i;i+=0.02){float c=sin(i),d=cos(j),e=
    sin(A),f=sin(j),g=cos(A),h=d+2,D=1/(c*
    h*e+f*g+5),l=cos      (i),m=cos(B),n=s\
    in(B),t=c*h*g-f*        e;int x=40+30*D*
    (l*h*m-t*n),y=            12+15*D*(l*h*n
    +t*m),o=x+80*y,          N=8*((f*e-c*d*g
    )*m-c*d*e-f*g-l        *d*n);if(22>y&&
    y>0&&x>0&&80>x&&D>z[o]){z[o]=D;;;b[o]=
    ".,-~:;=!*#$@"[N>0?N:0];}}/*#****!!-*/
      printf("\x1b[H");for(k=0;1761>k;k++)
      putchar(k%80?b[k]:10);A+=0.04;B+=
        0.02;}}/*****####*******!!=;:~
          ~::==!!!**********!!!==::-
            .,~~;;;========;;;:~-.
                ..,--------,*/
  

• 자바스크립트 코드

    (function() {
    var _onload = function() {
      var pretag = document.getElementById('d');
      var canvastag = document.getElementById('canvasdonut');
      var tmr1 = undefined, tmr2 = undefined;
      var A=1, B=1;
      var asciiframe=function() {
        var b=[];
        var z=[];
        A += 0.07;
        B += 0.03;
        var cA=Math.cos(A), sA=Math.sin(A),
            cB=Math.cos(B), sB=Math.sin(B);
        for(var k=0;k<1760;k++) {
          b[k]=k%80 == 79 ? "\n" : " ";
          z[k]=0;
        }
        for(var j=0;j<6.28;j+=0.07) {
          var ct=Math.cos(j),st=Math.sin(j);
          for(i=0;i<6.28;i+=0.02) {
            var sp=Math.sin(i),cp=Math.cos(i),
                h=ct+2,
            var x=0|(40+30*D*(cp*h*cB-t*sB)),
                y=0|(12+15*D*(cp*h*sB+t*cB)),
                o=x+80*y,
                N=0|(8*((st*sA-sp*ct*cA)*cB-sp*ct*sA-st*cA-cp*ct*sB));
            if(y<22 && y>=0 && x>=0 && x<79 && D>z[o])
            {
              z[o]=D;
              b[o]=".,-~:;=!*#$@"[N>0?N:0];
            }
          }
        }
        pretag.innerHTML = b.join("");
      };
      window.anim1 = function() {
        if(tmr1 === undefined) {
          tmr1 = setInterval(asciiframe, 50);
        } else {
          clearInterval(tmr1);
          tmr1 = undefined;
        }
      };
      var R1 = 1;
      var R2 = 2;
      var K1 = 150;
      var K2 = 5;
      var canvasframe=function() {
        var ctx = canvastag.getContext('2d');
        ctx.fillStyle='#000';
        ctx.fillRect(0, 0, ctx.canvas.width, ctx.canvas.height);
        if(tmr1 === undefined) { 
          A += 0.07;
          B += 0.03;
        }
        var cA=Math.cos(A), sA=Math.sin(A),
            cB=Math.cos(B), sB=Math.sin(B);
        for(var j=0;j<6.28;j+=0.3) { 
          var ct=Math.cos(j),st=Math.sin(j); 
          for(i=0;i<6.28;i+=0.1) {   
            var sp=Math.sin(i),cp=Math.cos(i); 
            var ox = R2 + R1*ct, 
            var x = ox*(cB*cp + sA*sB*sp) - oy*cA*sB; 
            var y = ox*(sB*cp - sA*cB*sp) + oy*cA*cB; 
            var ooz = 1/(K2 + cA*ox*sp + sA*oy); 
            var xp=(150+K1*ooz*x); 
            var yp=(120-K1*ooz*y); 
            var L=0.7*(cp*ct*sB - cA*ct*sp - sA*st + cB*(cA*st - ct*sA*sp));
            if(L > 0) {
              ctx.fillStyle = 'rgba(255,255,255,'+L+')';
              ctx.fillRect(xp, yp, 1.5, 1.5);
            }
          }
        }
      }
      window.anim2 = function() {
        if(tmr2 === undefined) {
          tmr2 = setInterval(canvasframe, 50);
        } else {
          clearInterval(tmr2);
          tmr2 = undefined;
        }
      };
      asciiframe();
      canvasframe();
    }
    if(document.all)
      window.attachEvent('onload',_onload);
    else
      window.addEventListener("load",_onload,false);
    })();